Lab 4: Recursion and Tree Recursion
Due at 11:59pm on 07/02/2015.
Starter Files
Download lab04.zip. Inside the archive, you will find starter files for the questions in this lab, along with a copy of the OK autograder.
Submission
By the end of this lab, you should have submitted the lab with
python3 ok --submit. You may submit more than once before the
deadline; only the final submission will be graded.
- To receive credit for this lab, you must complete Questions 1, 6, 7, 8, and 9 in lab04.py and submit through OK.
- Questions 2, 3, 4, and 5 are to show you what some common recursion misconceptions and mistakes are.
- Questions 10 is extra practice. It can be found in the lab04_extra.py file. It is recommended that you complete this problem on your own time.
Recursion
A recursive function is a function that calls itself in its body, either directly or indirectly. Recursive functions have three important components:
- Base case(s), the simplest possible form of the problem you're trying to solve.
- Consider a recursive call on a smaller argument.
- Recursive case(s), where the function calls itself with a simpler argument as part of the computation.
Let's look at the canonical example, factorial:
def factorial(n):
if n == 0:
return 1
return n * factorial(n - 1)We know by its definition that 0! is 1. So we choose n = 0 as our
base case. The recursive step also follows from the definition of
factorial, i.e. n! = n * (n-1)!.
The next few questions in lab will have you writing recursive functions. Here are some general tips:
- Consider how you can solve the current problem using the solution to a simpler version of the problem. Remember to trust the recursion: assume that your solution to the simpler problem works correctly without worrying about how.
- Think about what the answer would be in the simplest possible case(s). These will be your base cases - the stopping points for your recursive calls. Make sure to consider the possibility that you're missing base cases (this is a common way recursive solutions fail).
- It may help to write the iterative version first.
Question 1: Skip Add
Write a function skip_add that takes a single argument n
and computes the sum of every other integers between 0 and n
starting from n. Assume n is non-negative.
def skip_add(n):
""" Takes a number x and returns x + x-2 + x-4 + x-6 + ... + 0.
>>> skip_add(5) # 5 + 3 + 1 + 0
9
>>> skip_add(10) # 10 + 8 + 6 + 4 + 2 + 0
30
"""
"*** YOUR CODE HERE ***"
if n <= 0:
return 0
return n + skip_add(n - 2)Use OK to test your code:
python3 ok -q skip_addQuestion 2: Common Misconception
Fix the error with the following recursive function.
def count_up(n):
"""Print out all numbers up to and including n in ascending order.
>>> count_up(5)
1
2
3
4
5
"""
i = 1
if i == n:
return
print(i)
i += 1
count_up(n-1)The variable i resets back to 1 for each function call
and will print 1 each time. Try it out!
Question 3: Common Misconception
Fix the error with this recursive function.
def skip_mul(n):
"""Return the product of n * (n - 2) * (n - 4) * ...
>>> skip_mul(5) # 5 * 3 * 1
15
>>> skip_mul(8) # 8 * 6 * 4 * 2 * 0
0
"""
if n == 0:
return 0
else:
return n * skip_mul(n - 2)Consider what happens when we choose an odd number for n. skip_mul(3) will
return 3 * skip_mul(1). skip_mul(1) will return 1 * skip_mul(-1). You
may see the problem now. Since we are decreasing n by two at a time, we've
completed missed our base case of n == 0, and we will end up recursing
indefinitely. We need to add another base case to make sure this doesn't
happen.
def skip_mul(n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return n * skip_mul(n - 2)Question 4: Common Misconception
Fix the error with the following recursive function.
def factorial(n):
"""Return n * (n - 1) * (n - 2) * ... * 1.
>>> factorial(5)
120
"""
if n == 0:
return 1
else:
n * factorial(n-1)The result of the recursive calls is not returned.
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)Question 5: Common Misconception
Fix the error with the following recursive function:
def print_up_to(n):
"""Print every natural number up to n, inclusive.
>>> print_up_to(5)
1
2
3
4
5
"""
i = 1
if i > n:
return
else:
print(i)
i += 1
print_up_to(n)The function never reduces toward the base case of i == n.
def print_up_to(n):
def helper(i):
print(i)
if i < n:
helper(i + 1)
helper(1)Note:
- To keep track of info between recursive calls, we passsed the information as arguments to the function. This also allows us to get by without explicitly assigning a counter.
- The helper function doesn't have a base case written.
The base case is implicit because we have the condition
i < nWe will stop recursing oncei == nand we violate this condition.
Question 6: GCD
The greatest common divisor of two positive integers a and b is the
largest integer which evenly divides both numbers (with no remainder).
Euclid, a Greek mathematician in 300 B.C., realized that the greatest
common divisor of a and b is one of the following:
- the smaller value if it evenly divides the larger value, OR
- the greatest common divisor of the smaller value and the remainder of the larger value divided by the smaller value
In other words, if a is greater than b and a is not divisible by
b, then
gcd(a, b) == gcd(b, a % b)Write the gcd function recursively using Euclid's algorithm.
def gcd(a, b):
"""Returns the greatest common divisor of a and b.
Should be implemented using recursion.
>>> gcd(34, 19)
1
>>> gcd(39, 91)
13
>>> gcd(20, 30)
10
>>> gcd(40, 40)
40
"""
"*** YOUR CODE HERE ***"
a, b = max(a, b), min(a, b)
if a % b == 0:
return b
else:
return gcd(b, a % b)
# Iterative solution, if you're curious
def gcd_iter(a, b):
"""Returns the greatest common divisor of a and b, using iteration.
>>> gcd_iter(34, 19)
1
>>> gcd_iter(39, 91)
13
>>> gcd_iter(20, 30)
10
>>> gcd_iter(40, 40)
40
"""
if a < b:
return gcd_iter(b, a)
while a > b and not a % b == 0:
a, b = b, a % b
return bUse OK to test your code:
python3 ok -q gcdQuestion 7: Hailstone
For the hailstone function from homework 1, you pick a positive
integer n as the start. If n is even, divide it by 2. If n is
odd, multiply it by 3 and add 1. Repeat this process until n is 1.
Write a recursive version of hailstone that prints out the values of
the sequence and returns the number of steps.
def hailstone(n):
"""Print out the hailstone sequence starting at n, and return the
number of elements in the sequence.
>>> a = hailstone(10)
10
5
16
8
4
2
1
>>> a
7
"""
"*** YOUR CODE HERE ***"
print(n)
if n == 1:
return 1
elif n % 2 == 0:
return 1 + hailstone(n // 2)
else:
return 1 + hailstone(3 * n + 1)Use OK to test your code:
python3 ok -q hailstoneTree Recursion
A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree shaped process.
The classic example for tree recursion is fibonacci.

Question 8: Fibonacci
Write the fibonacci function using tree recursion.
The function should take in n and return the nth
fibonacci number.
As a reminder, Fibonacci is defined as a function where:
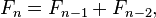
def fibonacci(n):
"""Return the nth fibonacci number.
>>> fibonacci(11)
89
>>> fibonacci(5)
5
>>> fibonacci(0)
0
>>> fibonacci(1)
1
"""
"*** YOUR CODE HERE ***"
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)Use OK to test your code:
python3 ok -q fibonacciQuestion 9: Insect Combinatorics
Consider an insect in an M by N grid. The insect starts at the
bottom left corner, (0, 0), and wants to end up at the top right
corner, (M-1, N-1). The insect is only capable of moving right or
up. Write a function paths that takes a grid length and width
and returns the number of different paths the insect can take from the
start to the goal. (There is a closed-form solution to this problem,
but try to answer it procedurally using recursion.)

For example, the 2 by 2 grid has a total of two ways for the insect to move from the start to the goal. For the 3 by 3 grid, the insect has 6 diferent paths (only 3 are shown above).
def paths(m, n):
"""Return the number of paths from one corner of an
M by N grid to the opposite corner.
>>> paths(2, 2)
2
>>> paths(5, 7)
210
>>> paths(117, 1)
1
>>> paths(1, 157)
1
"""
"*** YOUR CODE HERE ***"
if m == 1 or n == 1:
return 1
return paths(m - 1, n) + paths(m, n - 1)Use OK to test your code:
python3 ok -q pathsExtra Questions
Questions in this section are not required for submission. However, we encourage you to try them out on your own time for extra practice.
Question 10: Interleaved Sum
Recall that the summation function computes the sum of a sequence of
terms from 1 to n:
def summation(n, term):
"""Return the sum of the first n terms of a sequence.
>>> summation(5, lambda x: pow(x, 3))
225
"""
total, k = 0, 1
while k <= n:
total, k = total + term(k), k + 1
return totalWrite a function interleaved_sum that similarly computes the sum of a
sequence of terms from 1 to n, but uses different function to compute
the terms for odd and even numbers. Do so without using any loops or
testing in any way if a number is odd or even. (You may test if a
number is equal to 0, 1, or n.)
def interleaved_sum(n, odd_term, even_term):
"""Compute the sum odd_term(1) + even_term(2) + odd_term(3) + ..., up
to n.
>>> # 1 + 2^2 + 3 + 4^2 + 5
... interleaved_sum(5, lambda x: x, lambda x: x*x)
29
"""
"*** YOUR CODE HERE ***"
return interleaved_helper(n, odd_term, even_term, 1)
def interleaved_helper(n, term0, term1, k):
if k == n:
return term0(k)
return term0(k) + interleaved_helper(n, term1, term0, k+1)
# Alternate solution
def interleaved_sum2(n, odd_term, even_term):
"""Compute the sum odd_term(1) + even_term(2) + odd_term(3) + ..., up
to n.
>>> # 1 + 2^2 + 3 + 4^2 + 5
... interleaved_sum2(5, lambda x: x, lambda x: x*x)
29
"""
total, term0, term1 = interleaved_helper2(n, odd_term, even_term)
return total
def interleaved_helper2(n, odd_term, even_term):
if n == 1:
return odd_term(1), even_term, odd_term
else:
total, term0, term1 = interleaved_helper2(n-1, odd_term,
even_term)
return total + term0(n), term1, term0Use OK to test your code:
python3 ok -q interleaved_sum