Practice problems: Functions and Expressions

If you are studying for an exam, or you just want some extra practice with concepts in this class, you might find these practice problems helpful!

Question 1: Distance

Implement a function called distance(x1, y1, x2, y2):

x1 and y1 form an x-y coordinate pair
x2 and y2 form an x-y coordinate pair

distance returns the Euclidean distance between the two points. Use the following formula:

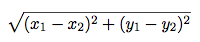
2-D distance formula

import sqrt

def distance(x1, y1, x2, y2):
    """Calculates the Euclidian distance between two points (x1, y1) and (x2, y2)

    >>> distance(1, 1, 1, 2)
    1.0
    >>> distance(1, 3, 1, 1)
    2.0
    >>> distance(1, 2, 3, 4)
    2.8284271247461903
    """
    "*** YOUR CODE HERE ***"
    return sqrt(square(x1-x2) + square(y1-y2))

Question 2: Distance (3-D)

Now, let us edit this program to get the distance between two 3-dimensional coordinates. Your distance3d function should take six arguments and compute the following:

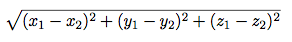
3-D distance formula

def distance3d(x1, y1, z1, x2, y2, z2):
    """Calculates the 3D Euclidian distance between two points (x1, y1, z1) and
    (x2, y2, z2).

    >>> distance3d(1, 1, 1, 1, 2, 1)
    1.0
    >>> distance3d(2, 3, 5, 5, 8, 3)
    6.164414002968976
    """
    "*** YOUR CODE HERE ***"
    return sqrt(square(x1-x2) + square(y1-y2) + square(z1-z2))

Question 3

Implement harmonic, which returns the harmonic mean of two positive numbers x and y. The harmonic mean of 2 numbers is 2 divided by the sum of the reciprocals of the numbers. (The reciprocal of x is 1/x.)

def harmonic(x, y):
    """Return the harmonic mean of x and y.

    >>> harmonic(2, 6)
    3.0
    >>> harmonic(1, 1)
    1.0
    >>> harmonic(2.5, 7.5)
    3.75


    >>> harmonic(4, 12)
    6.0
    """
    "*** YOUR CODE HERE ***"
    return 2/(1/x + 1/y)

Question 4: Environment diagrams

If you haven't found this gem already, tutor.composingprograms.com has a great visualization tool for environment diagrams. Paste in your Python code and it will generate an environment diagram you can walk through step-by-step! Use it to help you check your answers!

Try drawing environment diagrams for the following examples and predicting what Python will output:

>>> def square(x):
...     return x * x
>>> def double(x):
...     return x + x
>>> a = square(double(4))
>>> a
______
64

>>> x, y = 4, 3
>>> def reassign(arg1, arg2):
...     x = arg1
...     y = arg2
>>> reassign(5, 6)
>>> x
______
4
>>> y
______
3

>>> def f(x):
...     f(x)
>>> print, f = f, print
>>> a = f(4)
______
4
>>> a
______
# Nothing shows up, because a = None
>>> b = print(4)
______
4
>>> b
______
# Nothing shows up, because b = None