Diagnostic 2: Week 2 review

Recursion

Question 1: In summation...

Write the recursive version of summation, which takes two arguments, a number n and a function term, applies term to every number between 1 and n inclusive, and returns the sum of those results.

def summation(n, term):
    """Return the sum of the 0th to nth terms in the sequence defined
    by term.
    Should be implemented using recursion.

    >>> summation(5, lambda x: x * x * x)
    225
    >>> summation(9, lambda x: x + 1)
    55
    >>> summation(5, lambda x: 2**x)
    63
    """
    "*** YOUR CODE HERE ***"
    if n == 0:
        return term(0)
    return term(n) + summation(n - 1, term)

Question 2

Write a function has_seven that takes a positive integer n and returns whether n contains the digit 7. Do not use any assignment statements - use recursion instead:

def has_seven(k):
    """Returns True if at least one of the digits of k is a 7, False otherwise.

    >>> has_seven(3)
    False
    >>> has_seven(7)
    True
    >>> has_seven(2734)
    True
    >>> has_seven(2634)
    False
    >>> has_seven(734)
    True
    >>> has_seven(7777)
    True
    """
    "*** YOUR CODE HERE ***"
    if k % 10 == 7:
        return True
    elif k < 10:
        return False
    else:
        return has_seven(k // 10)

Question 3

An infinite continued fraction is an expression of the form:

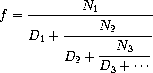
As an example, one can show that the inverse of the golden ratio can be computed by setting all of the terms to 1. A way to approximate the value of an infinite continued fraction is to compute the value of truncating after a given number of terms. This truncation, called the k-term finite continued fraction, has the form:

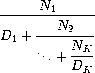
Write a function iterative_continued_frac, which takes two functions n_term and d_term, which each produce the ith N and D term respectively, and a number k and returns the k-term finite continued fraction. Use iteration to perform the computation.

def iterative_continued_frac(n_term, d_term, k):
    """Returns the k-term continued fraction with numerators defined by n_term
    and denominators defined by d_term.

    >>> # golden ratio
    ... round(iterative_continued_frac(lambda x: 1, lambda x: 1, 8), 3)
    0.618
    >>> # 1 / (1 + (2 / (2 + (3 / (3 + (4 / 4))))))
    ... round(iterative_continued_frac(lambda x: x, lambda x: x, 4), 6)
    0.578947
    """
    "*** YOUR CODE HERE ***"
    result, i = 0, k
    while i >= 1:
        result, i = n_term(i) / (d_term(i) + result), i-1
    return result

Now write a function recursive_continued_frac that uses recursion to compute the k-term finite continued fraction. Hint: try writing a recursive helper function to do most of the work, rather than trying to do the recursion with recursive_continued_frac directly.

def recursive_continued_frac(n_term, d_term, k):
    """Returns the k-term continued fraction with numerators defined by n_term
    and denominators defined by d_term.

    >>> # golden ratio
    ... round(recursive_continued_frac(lambda x: 1, lambda x: 1, 8), 3)
    0.618
    >>> # 1 / (1 + (2 / (2 + (3 / (3 + (4 / 4))))))
    ... round(recursive_continued_frac(lambda x: x, lambda x: x, 4), 6)
    0.578947
    """
    "*** YOUR CODE HERE ***"
    return recursive_continued_frac_helper(n_term, d_term, k, 1)

def recursive_continued_frac_helper(n_term, d_term, k, i):
    denom = d_term(i)
    if i < k:
        denom += recursive_continued_frac_helper(n_term, d_term, k, i+1)
    return n_term(i) / denom

Tree recursion

Question 4: Partition

The number of partitions of a positive integer n is the number of ways in which n can be expressed as the sum of positive integers in increasing order. For example, the number 5 has 7 partitions.

5 = 5
5 = 1 + 4
5 = 2 + 3
5 = 1 + 1 + 3
5 = 1 + 2 + 2
5 = 1 + 1 + 1 + 2
5 = 1 + 1 + 1 + 1 + 1

Write a tree-recursive function part(n) that returns the number of partitions of n.

Hint: Introduce a helper function that computes partitions of n using only a subset of the integers less than or equal to n. Once you have done so, you can use very similar logic to the count_change function from the lecture notes:

def part(n):
    """Return the number of partitions of positive integer n.

    >>> part(5)
    7
    >>> part(10)
    42
    >>> part(15)
    176
    >>> part(20)
    627
    """
    "*** YOUR CODE HERE ***"
    return part_max(n, n)

def part_max(n, m):
    """Return the number of partitions of n using integers up to m.

    >>> part_max(5, 3)
    5
    """ 
    if n < 0 or m <= 0:
        return 0
    if n == 0:
        return 1
    return part_max(n-m, m) + part_max(n, m-1)

def ten_pairs(n):
    """Return the number of ten-pairs within positive integer n.

    >>> ten_pairs(7823952)
    3
    >>> ten_pairs(55055)
    6
    >>> ten_pairs(9641469)
    6
    """
    "*** YOUR CODE HERE ***"
    if n < 10:
        return 0
    else:
        return ten_pairs(n//10) + count_digit(n//10, 10 - n%10)

def count_digit(n, digit):
    """Return how many times digit appears in n.

    >>> count_digit(55055, 5)
    4
    """
    if n == 0:
        return 0
    else:
        if n%10 == digit:
            return count_digit(n//10, digit) + 1
        else:
            return count_digit(n//10, digit)

def bar(n):
    i, sum = 1, 0
    while i <= n:
        sum += biz(n)
        i += 1
    return sum

def biz(n):
    i, sum = 1, 0
    while i <= n:
        sum += i**3
        i += 1
    return sum

def bonk(n):
    sum = 0
    while n >= 2:
        sum += n
        n = n / 2
    return sum